f(x)=
Una vez escrita dicha función en la barra con la que cuenta Wolframalpha
nos muestra dos gráficos de la función, pero yo solo tomaré para analizar el primero que va desde x=-3 hasta x=4
Dominio= R
(Observando el gráfico)
Imágen= R
(Observando el gráfico)
(Observando el gráfico)
Raíces= -3, -1, 2 y 3
Para obtenerlas observamos la forma alternativa de la función que nos da Wolframalpha, la cual es "(x-3)(x-2)(x+1)(x+3)" y tomamos como raíces a los valores q anulan a los valores dentro de los paréntesis. O si deseamos omitir este paso, podemos fijarnos en la parte del análisis del programa que dice "roots".
Ordenada al orígen= 18
Para obtenerla debemos igualar la función a cero, y la escribimos de tal forma en la barra de Wolframalpha
Para obtenerla debemos igualar la función a cero, y la escribimos de tal forma en la barra de Wolframalpha
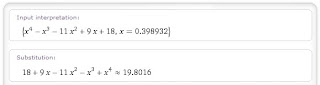
lo que hará que el programa sustituya las x por cero, así obtendremos el resultado que nos permitirá saber cuál es la ordenada al orígen.
Y quedaría de la siguiente manera: 18+9.0-11.0^2-0^3+0^4= 18
Conjunto de positividad= (-∞;-3) U (-1;2) U (3;∞)
(a partir de las raíces obtenidas)
(a partir de las raíces obtenidas)
Conjunto de negatividad= (-3;-1) U (2;3)
(a partir de las raíces obtenidas)
(a partir de las raíces obtenidas)
Máximo= (0,398982; 19,8016)
Mínimo= (-2,20582; -20,9672)
Obtenidos a partir de la derivada de la función, la cual es
f '(x)= 
Escribiéndola en la barra de Wolframalpha encontramos, entre otros datos, sus raíces. Detectando las dos que representan el valor de x en puntos críticos, sustituimos las x en la función original por dichos valores "0,398982" y "-2,20582" y nos dará el valor que toman en y en los puntos críticos (máximo/mínimo).
En el primer caso:
En el segundo caso:
Como todavía no sabemos cuál es el máximo y cuál es el mínimo debemos obtener la segunda derivada, derivando la derivada de la función original (escribimos la primera derivada en la barra de Wolframalpha).
f ''(x)= 
Una vez obtenida la segunda derivada, sustituimos los valores de las raíces de la primera derivada (pertenecientes a los puntos críticos) por las x de la segunda derivada.
En el primer caso, como el resultado de dicha sustitución fue menor a 0 sabemos que hay un
máximo. En el segundo caso, al resultar mayor a 0, hay un mínimo
máximo. En el segundo caso, al resultar mayor a 0, hay un mínimo
Intervalo de crecimiento= (-2,20582 ; 0,398982) U (2,55689 ; ∞)
Intervalo de decrecimiento= (-∞ ; -2,20582) U (0,398982 ; 2,55689)
